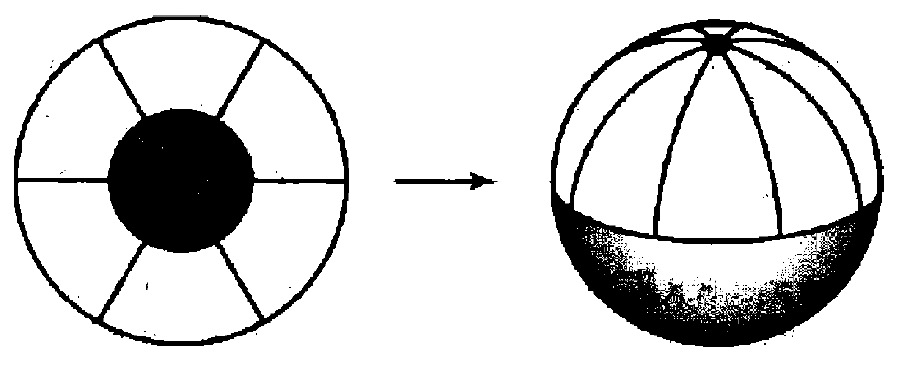
Ejemplos espacios cocientes

Ejemplo 1

Para el intervalo $I=[0,1]$, podemos considerar la partición:

El espacio cociente $(\tilde{I},\stackrel{\mathcal{~}}{\mathcal{T}})$ es homeomorfo a la circunferencia unidad ${\mathbb{S}}^1$. ^[1]

Ejemplo 2

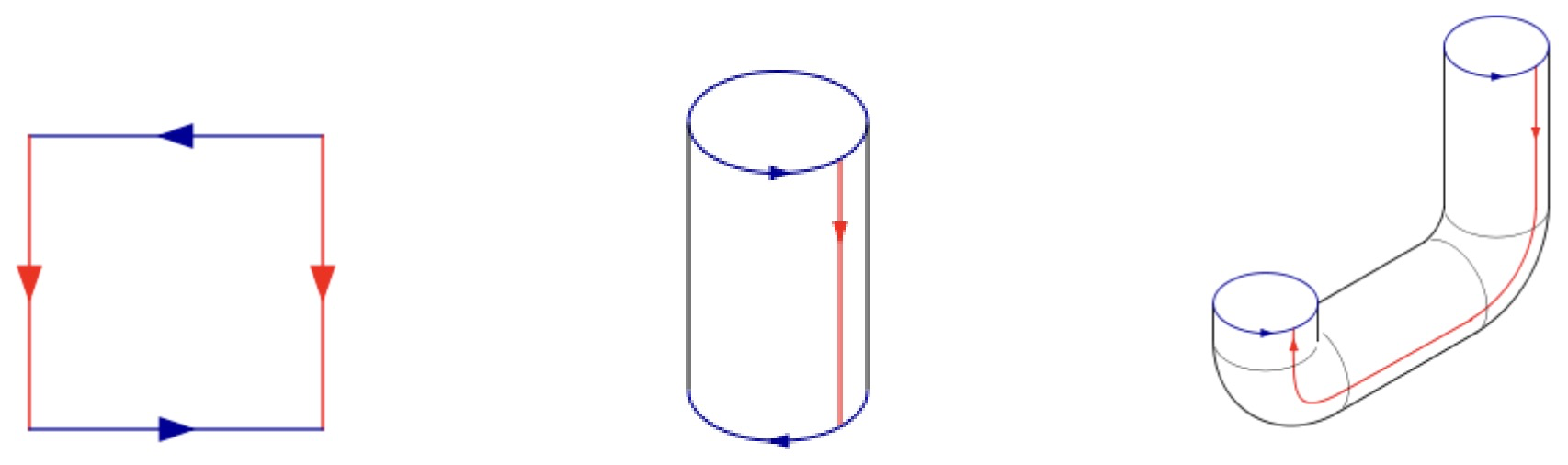
El cilindro es homeomorfo a $X=[0,1]\times [0,1]$ con la relación de equivalencia:

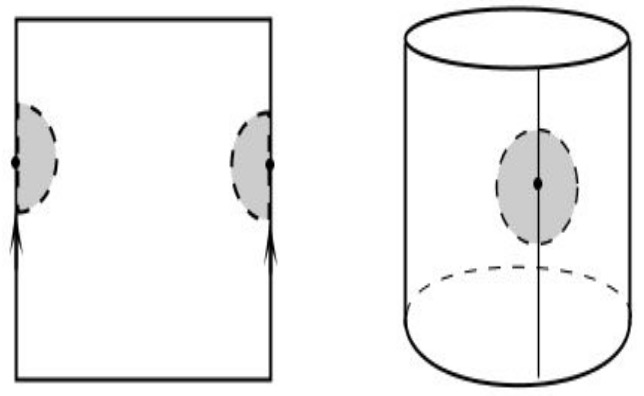
Ejemplo 3

La banda de Möbius es homeomorfa a $X=[0,1]\times [0,1]$ con la relación de equivalencia:

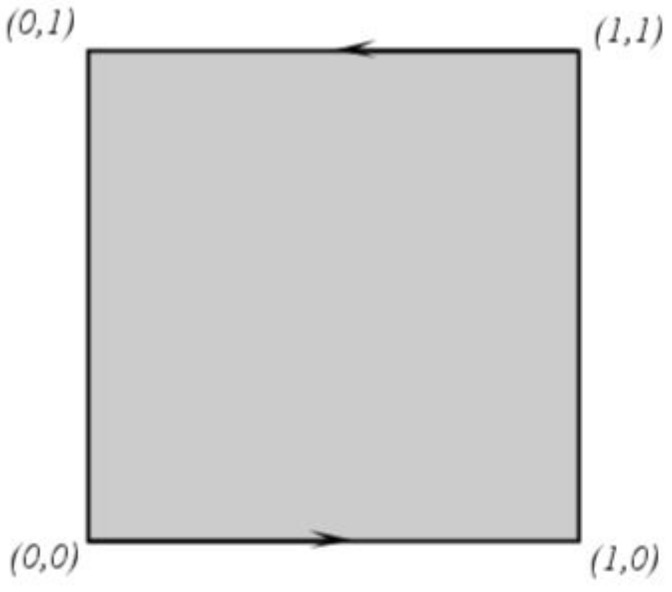
Ejemplo 4

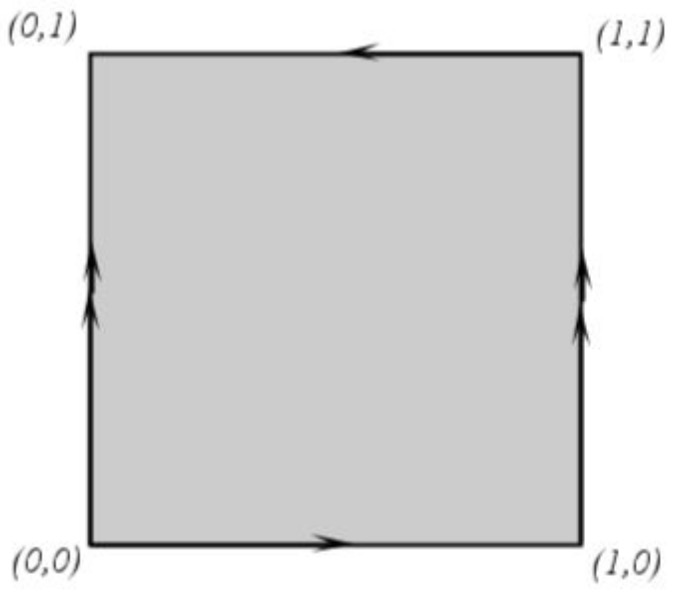
El toro es homeomorfo a $X=[0,1]\times [0,1]$ con la relación de equivalencia:

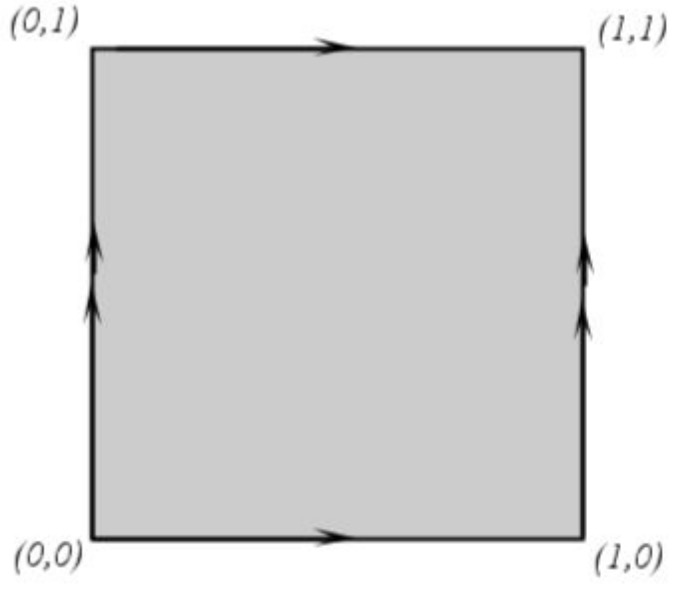
Ejemplo 5

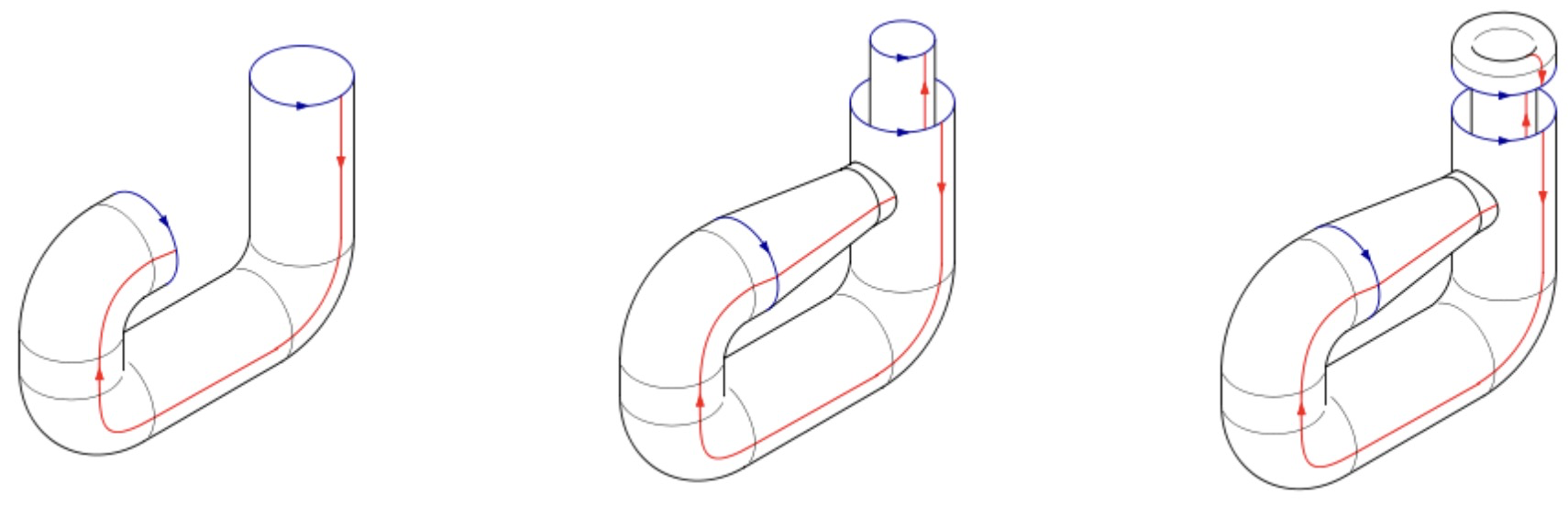
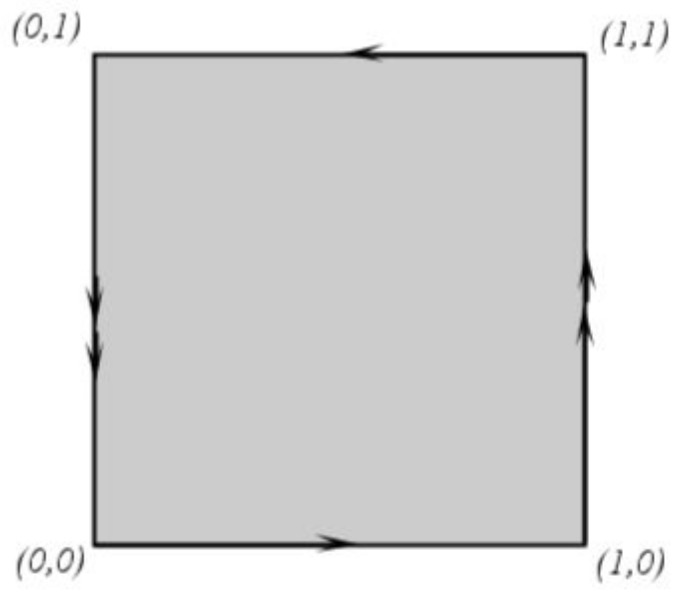
La botella de Klein es homeomorfa a $X=[0,1]\times [0,1]$ con la relación de equivalencia:

Ejemplo 6

El cono es homeomorfo a $X={\mathbb{S}}^1\times [0,1]$ con la relación de equivalencia:

Ejemplo 7

El plano proyectivo ${\mathbb{RP}}^2$ es homeomorfo a $X={\mathbb{S}}^2$ con la relación de equivalencia:

También es homeomorfo a $[0,1]\times [0,1]$ con la relación de equivalencia:

Ejemplo 8

El disco cerrado $\overline{D(0,1)}\subset {\mathbb{R}}^2$ con la relación de equivalencia

es homeomorfo a la esfera ${\mathbb{S}}^2$.